- Регистрация
- 23.09.18
- Сообщения
- 12.347
- Реакции
- 176
- Репутация
- 0
Привет! Меня зовут Рома, я работаю iOS-разработчиком в Exness. А кроме того, пишу на Clojure и инвестирую.
Сегодня я расскажу о том, как оценивать опционы. Это вводная статья и заработать миллион, используя предложенный способ, вряд ли получится. Тем не менее, это хорошая основа для понимания более сложных методов оценки.
Clojure
В основе языка лежат преобразования неизменяемых данных, а стандартная библиотека содержит
Кроме того, Clojure работает на JVM, а значит, доступны все финансовые библиотеки, написанные на Java.
Наконец,
Опционы
Я не буду углубляться в детали того, что такое
(defn call-option-value [security-price strike-price]
(Math/max (- security-price strike-price) 0))
;; examples
(call-option-value 360.0 280.0)
=> 80.0
(call-option-value 10.0 280.0)
=> 0.0
Понятно, что будущую цену базового инструмента мы не знаем. Тем не менее, нужно как-то определить стоимость опциона сегодня.
Большинство методов оценки строятся на простом принципе: мы пытаемся понять, какие результаты возможны, усредняем их, а затем дисконтируем результат.
Гипотетический
(-> (get-possible-outcomes) mean present-value))
Аналогично работает и метод Монте-Карло, только возможные результаты мы получаем путем проведения множества симуляций:
(-> (repeatedly n simulate-outcome) mean present-value)))
Монте-Карло
Напишем функцию, которая будет моделировать движение цены до момента экспирации опциона. Мы будем использовать вариант
Для начала, шаг цены:
(defn gbm-step [price dt rate volatility]
(let [drift (* price rate dt)
shock (* price volatility (Math/sqrt dt) (gaussian))
change (+ drift shock)]
(+ price change)))
;; next day price
(gbm-step 1200 1/365 0.01 0.15)
=> 1207.554940519062
Как видно из сигнатуры, кроме стартовой цены, нам также нужны безрисковая ставка и волатильность в годовом выражении. Мы будем использовать ставку по трежерам и историческую волатильность.
Так как цена на завтра зависит только от сегодняшней цены, можем воспользоваться функцией
Смоделируем движение цены акции Apple ($257) на следующие 100 дней:
(take 100 (iterate #(gbm-step % 1/365 0.01 0.15) 257))
=>
(257
258.6727911540819
256.91541924148663
252.98034966342195
251.1008036685261
...
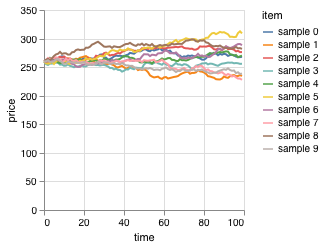
Запустим симуляцию 10 раз и посмотрим, что получилось:
После того, как мы научились прогнозировать цену базового инструмента на дату экспирации, используем ее для получения финансового результата по опциону:
(defn simulate-outcome [price strike rate volatility expiration]
(let [steps 100
dt (/ expiration steps)
prices (iterate #(gbm-step % dt rate volatility) price)
price-at-expiration (last (take steps prices))]
(call-option-value price-at-expiration strike)))
;; simulate 5 outcomes for one option
(repeatedly 5 #(simulate-outcome 1924 1925 0.01 0.45 0.5))
=> (0.0 730.6715047778875 329.1915857113486 0.0 0.0)
Экспирация здесь измеряется в долях года. То есть, для опциона, исполняющегося через год, она равна 1.
Наконец, основной интерфейс:
(defn evaluate-call-option [& {:keys [security-price strike-price risk-free-rate volatility expiration]}]
(let [expiration (year-fraction-until expiration)
simulate-fn (partial simulate-outcome security-price strike-price risk-free-rate volatility expiration)
n 1000]
(-> (repeatedly n simulate-fn) mean (present-value risk-free-rate expiration))))
;; example
(evaluate-call-option
:security-price 1924
:strike-price 1925
:risk-free-rate 0.01
:volatility 0.45
:expiration (LocalDate/of 2020 4 17))
=> 74.66533445636996
Попробуем оценить опционы на Amazon со страйком от 2100 до 2140 и экспирацией 17 апреля:
(for [strike (range 2100 2150 10)]
(evaluate-call-option
:security-price 1987
:strike-price strike
:risk-free-rate 0.01
:volatility 0.35
:expiration (LocalDate/of 2020 4 17)))
=> (23.9 21.1 16.4 15.5 15.3)
А вот рыночные цены на момент написания:
=> (22.9 20.6 18.35 16.4 14.6 13.6)
Несмотря на простоту метода, нам удалось достаточно близко к ним подойти.
Заключение
На этом все. Код проекта доступен по
Ссылки
Сегодня я расскажу о том, как оценивать опционы. Это вводная статья и заработать миллион, используя предложенный способ, вряд ли получится. Тем не менее, это хорошая основа для понимания более сложных методов оценки.

Clojure
You must be registered for see links
В основе языка лежат преобразования неизменяемых данных, а стандартная библиотека содержит
You must be registered for see links
для этого, что очень помогает при решении финансовых задач.Кроме того, Clojure работает на JVM, а значит, доступны все финансовые библиотеки, написанные на Java.
Наконец,
You must be registered for see links
. Если вы не работали с Clojure, представьте Jupyter Notebook на стероидах. Можно писать код в полноценной
You must be registered for see links
и при этом постоянно взаимодействовать с запущенной программой.Опционы
Я не буду углубляться в детали того, что такое
You must be registered for see links
, и как он работает – на Хабре много статей на эту тему. Ограничимся функцией, которая определяет результат колл-опциона на дату его экспирации:(defn call-option-value [security-price strike-price]
(Math/max (- security-price strike-price) 0))
;; examples
(call-option-value 360.0 280.0)
=> 80.0
(call-option-value 10.0 280.0)
=> 0.0
Понятно, что будущую цену базового инструмента мы не знаем. Тем не менее, нужно как-то определить стоимость опциона сегодня.
Большинство методов оценки строятся на простом принципе: мы пытаемся понять, какие результаты возможны, усредняем их, а затем дисконтируем результат.
Гипотетический
You must be registered for see links
на Clojure выглядит так:(-> (get-possible-outcomes) mean present-value))
Аналогично работает и метод Монте-Карло, только возможные результаты мы получаем путем проведения множества симуляций:
(-> (repeatedly n simulate-outcome) mean present-value)))
Монте-Карло
Напишем функцию, которая будет моделировать движение цены до момента экспирации опциона. Мы будем использовать вариант
You must be registered for see links
.Для начала, шаг цены:
(defn gbm-step [price dt rate volatility]
(let [drift (* price rate dt)
shock (* price volatility (Math/sqrt dt) (gaussian))
change (+ drift shock)]
(+ price change)))
;; next day price
(gbm-step 1200 1/365 0.01 0.15)
=> 1207.554940519062
Как видно из сигнатуры, кроме стартовой цены, нам также нужны безрисковая ставка и волатильность в годовом выражении. Мы будем использовать ставку по трежерам и историческую волатильность.
Так как цена на завтра зависит только от сегодняшней цены, можем воспользоваться функцией
You must be registered for see links
для получения всех будущих цен.Смоделируем движение цены акции Apple ($257) на следующие 100 дней:
(take 100 (iterate #(gbm-step % 1/365 0.01 0.15) 257))
=>
(257
258.6727911540819
256.91541924148663
252.98034966342195
251.1008036685261
...
Запустим симуляцию 10 раз и посмотрим, что получилось:

После того, как мы научились прогнозировать цену базового инструмента на дату экспирации, используем ее для получения финансового результата по опциону:
(defn simulate-outcome [price strike rate volatility expiration]
(let [steps 100
dt (/ expiration steps)
prices (iterate #(gbm-step % dt rate volatility) price)
price-at-expiration (last (take steps prices))]
(call-option-value price-at-expiration strike)))
;; simulate 5 outcomes for one option
(repeatedly 5 #(simulate-outcome 1924 1925 0.01 0.45 0.5))
=> (0.0 730.6715047778875 329.1915857113486 0.0 0.0)
Экспирация здесь измеряется в долях года. То есть, для опциона, исполняющегося через год, она равна 1.
Наконец, основной интерфейс:
(defn evaluate-call-option [& {:keys [security-price strike-price risk-free-rate volatility expiration]}]
(let [expiration (year-fraction-until expiration)
simulate-fn (partial simulate-outcome security-price strike-price risk-free-rate volatility expiration)
n 1000]
(-> (repeatedly n simulate-fn) mean (present-value risk-free-rate expiration))))
;; example
(evaluate-call-option
:security-price 1924
:strike-price 1925
:risk-free-rate 0.01
:volatility 0.45
:expiration (LocalDate/of 2020 4 17))
=> 74.66533445636996
Попробуем оценить опционы на Amazon со страйком от 2100 до 2140 и экспирацией 17 апреля:
(for [strike (range 2100 2150 10)]
(evaluate-call-option
:security-price 1987
:strike-price strike
:risk-free-rate 0.01
:volatility 0.35
:expiration (LocalDate/of 2020 4 17)))
=> (23.9 21.1 16.4 15.5 15.3)
А вот рыночные цены на момент написания:
=> (22.9 20.6 18.35 16.4 14.6 13.6)
Несмотря на простоту метода, нам удалось достаточно близко к ним подойти.
Заключение
На этом все. Код проекта доступен по
You must be registered for see links
. В следующей статье я расскажу о том, как сделать кросс-платформенный десктопный интерфейс с помощью библиотеки
You must be registered for see links
и использовать его для отображения портфеля опционов.Ссылки
-
You must be registered for see links
-
You must be registered for see links
-
You must be registered for see links
-
You must be registered for see links
-
You must be registered for see links



