- Регистрация
- 23.09.18
- Сообщения
- 12.347
- Реакции
- 176
- Репутация
- 0

Пока другие компании обсуждают управление коллективом на удаленке, мы в Smart Engines продолжаем делиться с вами своим стеком технологий. Сегодня про оптимизацию нейронных сетей. Сделать систему распознавания на основе нейронных сетей, которая могла бы быстро работать на смартфонах и прочих мобильных устройствах – крайне непросто. А сделать так, чтобы при этом качество было высоким – еще сложнее. В этой статье мы расскажем о простом методе регуляризации нейронных сетей, используемом нами в Smart Engines для улучшения качества «мобильных» сетей с малым числом параметров. Идея метода основана на постепенном уменьшении линейной зависимости фильтров в сверточных слоях во время обучения, благодаря чему каждый нейрон работает более эффективно, и следовательно, улучшается обобщающая способность модели. Для этого мы в представляем фильтры в виде одномерных векторов и ортогонализируем пару с наибольшей длиной проекции друг на друга.
При проектировании большинства современных нейронных сетей подразумевается, что они будут выполняться где-нибудь удаленно на сервере, а данные для обработки будут поступать через клиент на ПК или мобильном устройстве. Однако такой подход недопустим, когда речь заходит о безопасности личных данных, передавать которые куда-либо не хочется (например, фото паспорта или банковской карты для распознавания). К счастью для нас, мобильные устройства сегодня обладают достаточными мощностями для запуска нейронных сетей, благодаря чему можно избежать пересылки данных третьим лицам. Другое дело, что эти сети должны быть небольшими и содержать малое количество операций, чтобы не испытывать терпение пользователя. Такие условия ограничивают максимально достижимое качество их работы, и какими способами можно улучшать “легкие” сети без ущерба для времени выполнения – открытый вопрос. Размышляя над этим, нами был придуман новый метод регуляризации в нейронных сетях, ориентированный на компактные сети и заключающийся в ортогонализации сверточных фильтров.
Пост является краткой версией доклада «Convolutional neural network weights regularization via orthogonalization», представленного в ноябре 2019 года на международной конференции ICMV 2019, г. Амстердам, Нидерланды.
Идея регуляризации с помощью ортогонализации
Так как предлагаемый метод относится к регуляризации, сначала напомним вкратце что это такое. Регуляризация заключается в накладывании на модель некоторых ограничений на основе наших представлений о том, как должна решаться поставленная задача. Как результат – повышается обобщающая способность сети. Например, L1 регуляризация способствует занулению части весов делая сеть разряженной, L2 – сдерживает значения коэффициентов в пределах малых чисел, Dropout устраняет зависимости отдельных нейронов, и т.д. Эти методы являются неотъемлемой частью процесса обучения многих современных сетей, особенно если они содержат большое число параметров – регуляризация позволяет достаточно неплохо бороться с переобучением.
Теперь вернемся к нашему методу. Оговоримся сразу, что прежде всего мы рассматриваем задачу классификации изображений сверточной нейронной сетью. Предположение, на основе которого мы пришли к использованию ортогонализации, следующее: если сеть крайне ограничена в своих ресурсах для понятия закономерностей в данных, то нужно заставить каждый нейрон в ней работать максимально эффективно, и чтобы он выполнял строго отведенную ему функцию. Иначе говоря, чтобы он “выцеплял” такие особенности, которые любой другой нейрон обнаружить неспособен. Решаем мы эту задачу за счет постепенного уменьшения линейной зависимости между векторами весов нейронов во время обучения. Для этого мы модифицировали классический алгоритм ортогонализации, адаптировав его под реалии процесса обучения.
Ортогонализация сверточных фильтров
Определим фильтры сверточного слоя как множество векторов

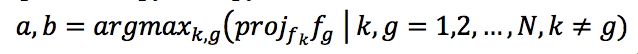
Проекция вектора f[SUB]g[/SUB] на f[SUB]k[/SUB] может быть вычислена как
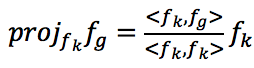
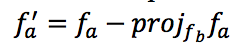
следующей формулой:

где η это скорость обучения и wort коэффициент ортогонализации, значения которого лежат на отрезке [0.0, 1.0]. Введение коэффициента ортогонализации обусловлено тем, что “мгновенная” ортогонализация фильтров сильно ломает процесс обучения, сводя на нет планомерные изменения весов за прошлые итерации. Малые значения wort сохраняют динамику обучения и способствуют плавному уменьшению линейной зависимости между фильтрами в каждом слое по отдельности. Отметим еще раз важный момент в методе: за одну итерацию мы модифицируем только один вектор, чтобы не навредить алгоритму оптимизации.

Рис. Визуализация одной итерации.
Мы рассматриваем ортогонализацию только сверточных фильтров, так как в современных нейронных сетях сверточные слои составляют большую часть архитектуры. Однако, алгоритм легко обобщается и на веса нейронов в полносвязных слоях.
Эксперименты
Перейдем от теории к практике. Для экспериментов мы решили использовать 2 самых популярных датасета для оценки нейросетей в области компьютерного зрения – MNIST (классификация изображений рукописных цифр) и CIFAR10 (фотографии 10 классов – лодки, грузовики, лошади, и т.д.).
Так как мы предполагаем, что ортогонализация будет полезна в первую очередь для компактных сетей, мы взяли LeNet подобную архитектуру в 3 модификациях, отличающихся друг от друга количеством фильтром в сверточных слоях. Архитектура нашей сети, которую для удобства назовем LeNet 1.0, приведена в таблице 1. Производные от нее архитектуры LeNet 2.0 и LeNet 3.5 отличаются большим числом фильтров в сверточных слоях, в 2 и в 3.5 раза соответственно.
Выбирая функцию активации, мы остановились на ReLU не только по причине того, что это самая популярная и вычислительно эффективная функция (напоминаем, что мы все еще говорим про быстрые сети). Дело в том, что применение не кусочно-линейных функций сводит на нет эффект ортогонализации: например, гиперболический тангенс сильно искажает входные вектора так как имеет ярко выраженную нелинейность в областях, близких к насыщению.
Таблица 1. Архитектура сети LeNet 1.0, используемая в экспериментах.
Слои | � | ||
# | Тип | Параметры | Функция активации |
1 | conv | 8 filters 3x3, stride 1x1, no padding | ReLU |
2 | conv | 16 filters 5x5, stride 2x2, padding 2x2 | ReLU |
3 | conv | 16 filters 3x3, stride 1x1, padding 1x1 | ReLU |
4 | conv | 32 filters 5x5, stride 2x2, padding 2x2 | ReLU |
5 | conv | 32 filters 3x3, stride 1x1, padding 1x1 | ReLU |
6 | conv | 32 filters 3x3, stride 1x1, padding 1x1 | ReLU |
7 | fully connected | 10 neurons | Softmax |
Мы пробовали 3 значения коэффициента ортогонализации wort: 0.01, 0.05, 0.1. Все эксперименты были проведены по 10 раз, а результаты усреднены (среднеквадратичное отклонение (std) для error rate приведено в таблице c результатами). Также мы посчитали, на сколько процентов уменьшилось число ошибок (benefit).
Результаты экспериментов подтвердили, что улучшение от ортогонализации тем больше, чем меньше параметров в сети (таблицы 2 и 3). Также нами был получен интересный результат, что использование ортогонализации в случае “тяжелых” сетей приводит к ухудшению качества.
Таблица 2. Результаты экспериментов для MNIST
MNIST | LeNet 1.0 (52k params) | LeNet 2.0 (179k params) | LeNet 3.5 (378k params) | � | |||||
error rate | std | benefit | error rate | std | benefit | error rate | std | benefit | � |
baseline | 0.402% | 0.033 | - | 0.366% | 0.026 | - | 0.361% | 0.028 | - |
wort=0.01 | 0.379% | 0.027 | 5.72% | 0.355% | 0.01 | 3.01% | 0.359% | 0.026 | 0.55% |
wort=0.05 | 0.36% | 0.022 | 10.45% | 0.354% | 0.018 | 3.28% | 0.356% | 0.034 | 1.39% |
wort=0.1 | 0.368% | 0.015 | 8.46% | 3.53% | 0.024 | 3.55% | 0.353% | 0.018 | 2.22% |
Таблица 3. Результаты экспериментов для CIFAR10
CIFAR10 | LeNet 1.0 (52k params) | LeNet 2.0 (179k params) | LeNet 3.5 (378k params) | � | |||||
error rate | std | benefit | error rate | std | benefit | error rate | std | benefit | � |
baseline | 22.09% | 0.65 | - | 18.49% | 1.01 | - | 17.08% | 0.47 | - |
wort=0.01 | 21.56% | 0.86 | 2.38% | 18.14% | 0.65 | 1.89% | 17.33% | 0.49 | -1.46% |
wort=0.05 | 21.59% | 0.48 | 2.24% | 18.30% | 0.57 | 1.03% | 17.59% | 0.31 | -3.02% |
wort=0.1 | 21.54% | 0.41 | 2.48% | 18.15% | 0.53 | 1.85% | 17.53% | 0.4 | -2.63% |
Однако, LeNet сети сейчас встречаются редко и обычно используются более современные модели. Поэтому, мы также экспериментировали с облегченной по количеству фильтров моделью ResNet, состоящей из 25 сверточных слоев. Первые 7 слоев содержали по 4 фильтра, следующие 12 по 8 фильтров, и последние 6 по 16 фильтров. Общее число обучаемых параметров такой модели составило 21 тыс. Результат получился аналогичным: ортогонализация улучшает качество сети.

Рис. Сравнение динамики обучения ResNet на MNIST с ортогонализацией и без.
Несмотря на достигнутые улучшения в качестве, для полной уверенности в корректной работе предлагаемого метода нужно посмотреть, какие изменения произошли в самих фильтрах. Для этого были отписаны значения максимальной длины проекции фильтров во 2, 12 и 25 слоях ResNet’а на всех эпохах обучения. Динамику изменений мы приводим на графиках ниже. Самое главное тут то, что во всех слоях наблюдается уменьшение линейной зависимости фильтров.
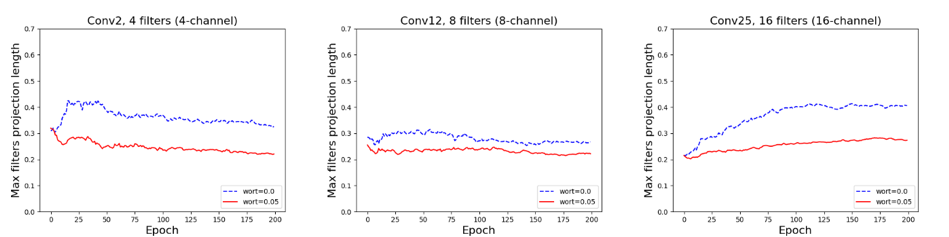
Рис. Динамика изменений максимальной длины проекции фильтров в сверточном слое на примере ResNet.
Регуляризация на основе ортогонализации крайне проста в имплементации: на питоне с помощью модуля numpy она занимает меньше 10 строк кода. При этом, она не замедляет обучение и совместима с другими методами регуляризации.
Заключение
Несмотря на свою простоту, ортогонализация помогает улучшить качество “легких” сетей, на которые наложены ограничения на размер и скорость выполнения. Ввиду распространения мобильных технологий, подобные ограничения возникают все чаще: нейронная сеть должна выполняться не где-то в облаке, а прямиком на устройстве со слабым процессором и малым количеством памяти. Обучение таких сетей идет в разрез со современными тенденциями в нейросетевой науке, где активно используются ансамбли моделей с миллионами обучаемых параметров, которые не потянет ни один смартфон. Именно поэтому, в рамках решения индустриальных задач, крайне важно придумывать и развивать методы улучшения качества простых и быстрых сетей.
Список используемых источников
Alexander V. Gayer, Alexander V. Sheshkus, «Convolutional neural network weights regularization via orthogonalization,» Proc. SPIE 11433, Twelfth International Conference on Machine Vision (ICMV 2019), 1143326 (31 January 2020);
You must be registered for see links



